Transformación bidimensional

La transformación bidimensional es el proceso de modificar una imagen en un plano según ciertas reglas matemáticas. Se utiliza para crear diferentes representaciones de la realidad o de la imaginación. Las transformaciones bidimensionales pueden alterar la posición, el tamaño, la forma o la orientación de la imagen original. También se pueden combinar entre sí para obtener efectos más complejos.

Existen diferentes tipos de transformaciones bidimensionales, como la traslación, el escalado, el sesgado y la rotación. Cada una de ellas modifica la imagen de una manera distinta.

Traslación

Definición

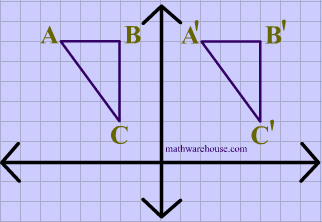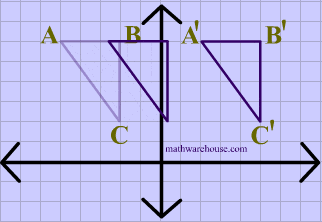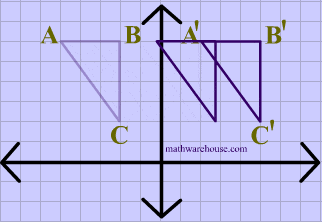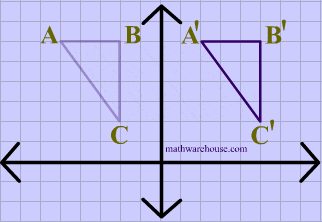
La traslación describe el desplazamiento de un objeto geométrico de una posición a otra, siguiendo una trayectoria lineal en un plano. Este tipo de transformación se realiza sin rotar ni voltear la figura, lo que significa que la forma y orientación del objeto se mantienen inalteradas durante el proceso. En esencia, la traslación se asemeja a deslizar o mover un objeto a lo largo de una línea recta desde una ubicación inicial en un sistema de coordenadas a una nueva ubicación en el mismo sistema de coordenadas. La figura sigue siendo idéntica en términos de su forma y tamaño, pero se encuentra en un lugar diferente en el plano. La traslación se define mediante un vector de traslación que indica la distancia y la dirección del movimiento del objeto en el plano, lo que permite representar el cambio de posición del objeto de manera precisa.

Características

• Desplazamiento de Puntos: La traslación implica mover un punto desde su posición original (X, Y) a una nueva posición (x', y') mediante la adición de distancias de traslación, Tx y Ty, a las coordenadas originales. Esto se expresa matemáticamente como x' = x + Tx y y' = y + Ty.
• Vector de Traslación: El par de distancias de traslación (Tx, Ty) se conoce como el vector de traslación o vector de cambio. Este vector indica la magnitud y la dirección en la que se debe mover el objeto.
• Aplicación a Polígonos: Para trasladar polígonos, se agregan las distancias de traslación especificadas a las coordenadas de cada punto extremo de las líneas que conforman el objeto. Esto permite mover el polígono en su totalidad sin cambiar su forma.
• Traslación de Objetos con Curvas: En el caso de objetos trazados con curvas, como círculos o elipses, se trasladan cambiando las coordenadas definitorias del objeto. Para mover la posición de una circunferencia o elipse, se ajustan las coordenadas del centro y se vuelve a dibujar la figura en su nueva ubicación.
• Valores de Distancia de Traslación: Las distancias de traslación pueden ser especificadas como cualquier número real, lo que incluye valores positivos, negativos o cero. Esto permite mover objetos en diversas direcciones y magnitudes.
• Consideraciones de Límites: Si un objeto se traslada más allá de los límites del área de visualización en las coordenadas del dispositivo, pueden ocurrir situaciones como la generación de mensajes de error, la supresión de partes del objeto que sobrepasan los límites o la presentación de una imagen distorsionada, dependiendo de cómo esté implementado.

Representación

En forma de coordenadas cartesianas:

En forma matricial:

Ejemplos

• La figura sigue viéndose exactamente igual, solo que en un lugar diferente. Se aplica una transformación en un objeto para cambiar su posición a lo largo de la trayectoria de una línea recta de una dirección de coordenadas a otra. 

• Se realiza una traslación de un punto sencillo de coordenadas, mediante la inclusión de compensaciones en sus propias coordenadas, para generar una nueva posición de coordenadas. Se está moviendo la posición del punto original a lo largo de una trayectoria en línea recta hacia su nueva localización.

Escalamiento

Definición

El escalamiento en transformación bidimensional en graficación se refiere a una operación que altera el tamaño de un objeto, ya sea haciéndolo más grande o más pequeño en su longitud, y se utiliza para modificar las dimensiones de un objeto de manera proporcional. Esta transformación se logra mediante la aplicación de factores de escala, Sx y Sy, a lo largo de las direcciones x e y, respectivamente. Además, se utiliza un punto o eje de referencia como centro de la operación.

En esencia, el escalamiento permite cambiar las dimensiones de un objeto manteniendo su forma y proporciones, lo que puede resultar en un efecto de zoom. El factor de escala Sx determina el cambio en tamaño en la dirección horizontal (x), mientras que el factor de escala Sy controla el cambio en tamaño en la dirección vertical (y).

Características

• Valores de Escala Flexibles: Los factores de escala, Sx y Sy, pueden tomar cualquier valor numérico positivo. Esto brinda flexibilidad para ajustar el tamaño de los objetos según las necesidades del diseño gráfico.
• Reducción de Tamaño: Cuando los valores de Sx y Sy son menores que 1, el objeto experimenta un escalamiento que reduce su tamaño en relación con las dimensiones originales. Esto permite disminuir las dimensiones de un objeto de forma proporcional.
• Agrandamiento: Por otro lado, cuando los valores de Sx y Sy son mayores que 1, el objeto se escala de manera que aumenta su tamaño en relación con las dimensiones originales. Este proceso de agrandamiento puede utilizarse para hacer que los objetos sean más grandes.
• Mantenimiento del Tamaño Original: Si se asigna un valor de 1 tanto a Sx como a Sy, el tamaño del objeto permanece inalterado. Esto permite mantener el tamaño original de los objetos sin cambiar sus dimensiones.

Tipos de escalamiento

Existen dos tipos de escalamiento:

• Escalamiento Uniforme: donde los factores de escala Sx y Sy son iguales, lo que significa que el objeto se agranda o reduce de manera uniforme en todas las direcciones. Esto preserva las proporciones internas del objeto. Si Sx = Sy = 1, el objeto no cambia de tamaño. Si ambos factores son mayores que 1, el objeto se agranda uniformemente en todas las direcciones; si son menores que 1, el objeto se reduce uniformemente.
• Escalamiento diferencial: donde los factores de escala Sx y Sy pueden ser diferentes, lo que significa que el objeto se agranda o reduce de manera diferente en las direcciones x e y. Esto altera las proporciones originales del objeto, ya que una dimensión se modifica más que la otra. El escalamiento no uniforme es útil cuando se necesita ajustar las dimensiones de un objeto de manera independiente a lo largo de diferentes ejes. 

Representación

Se usa un punto fijo, y se escala a partir de él, esto en coordenadas cartesianas:

En forma matricial seria de la siguiente forma:

Ejemplos

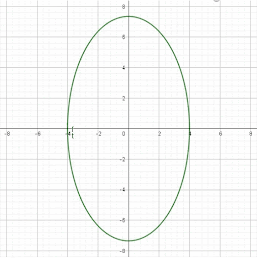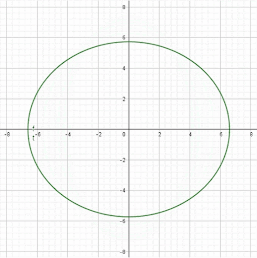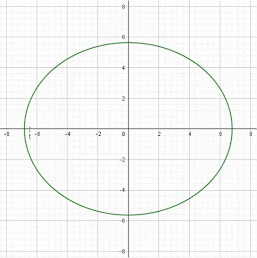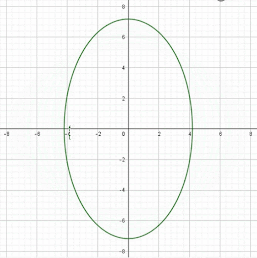
• Mediante la transformación del objeto, se puede percibir que con ella se consigue el efecto Zoom.

• Se escala a ½ en el eje x y a ¼ en el eje y, el escalamiento se efectúa con respecto al origen:

Rotación

Definición

La rotación es un proceso que implica la transformación de puntos de un objeto ubicados en trayectorias circulares. Esta transformación se caracteriza por un ángulo de rotación, que determina cuánto girará cada vértice de un polígono o cualquier otro objeto bidimensional.

Se pueden hacer que los objetos giren alrededor de un punto arbitrario o el punto pivote de la transformación de rotación puede colocarse en cualquier parte en el interior o fuera de la frontera exterior de un objeto, el efecto de la rotación consiste en oscilar el objeto con respecto a este punto interno. 

Características

• Ángulo de Rotación y Punto de Rotación: Para realizar una rotación, se especifica el ángulo de rotación, que puede ser tanto positivo como negativo, y el punto de rotación (pivote) alrededor del cual el objeto será rotado. El punto de rotación actúa como el centro de la rotación y es fundamental para determinar cómo se transforma el objeto.
• Sentido de Rotación: Los ángulos de rotación positivos definen una rotación en sentido contrario a las manecillas del reloj, es decir, una rotación en dirección antihoraria sobre el punto pivote, que generalmente se representa desde el eje X1 al eje X2. Por otro lado, los ángulos de rotación negativos producen una rotación en sentido de las manecillas del reloj, es decir, una rotación en dirección horaria, generalmente representada desde el eje X2 al eje X1.
• Mantenimiento de Forma y Tamaño: Las rotaciones son movimientos directos, lo que significa que mantienen la forma y el tamaño de las figuras originales. Esto permite girar objetos sin distorsionar sus proporciones.
• Sentido de Rotación Positivo y Negativo: El sentido de rotación puede ser positivo (en contra del sentido horario) o negativo (a favor del sentido horario). Esto proporciona flexibilidad para controlar la dirección en la que los objetos giran alrededor del punto pivote.

Representación

Pueden ser representados con respecto a un origen:

Pueden ser representados cuando el punto a rotar no es el origen y en el plano cartesiano:

De forma matricial:

Ejemplos

• En la figura se muestra la rotación de la casa 45º, con respecto al origen.

• Para rotar polígonos de cualquier tipo, debemos solo rotar cada uno de sus vértices y se redibuja.

Sesgado

Definición

El sesgo es a un tipo de transformación no rígida que implica la deformación del objeto original al aplicar esta transformación. En el sesgo, el objeto experimenta una distorsión que lo desplaza en una dirección específica, lo que da como resultado un objeto modificado con una inclinación. 

Características

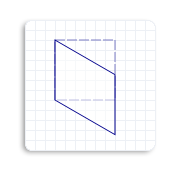
• Deformación No Rígida: El sesgo es una transformación no rígida, lo que significa que modifica la forma del objeto original. A diferencia de las transformaciones rígidas como la traslación, rotación y escalamiento, que preservan la forma y el tamaño del objeto, el sesgo provoca una deformación en el objeto al inclinarlo en una dirección específica.
• Inclinación en Direcciones Específicas: El sesgo puede ocurrir en dos direcciones principales: sesgo horizontal y sesgo vertical. El sesgo horizontal implica inclinar el objeto a lo largo del eje X (horizontal), mientras que el sesgo vertical implica inclinar el objeto a lo largo del eje Y (vertical).
• Preservación de la Proporción Relativa: Aunque el sesgo deforma la forma del objeto, preserva la proporción relativa entre sus partes. Las relaciones proporcionales entre diferentes partes del objeto se mantienen después de aplicar la transformación de sesgo. A pesar de la inclinación, las proporciones entre las dimensiones del objeto se conservan.

Tipos

• Sesgo Horizontal o en eje "x": El sesgo horizontal se refiere a la deformación o inclinación del objeto en la dirección horizontal, es decir, a lo largo del eje X. Al aplicar un sesgo horizontal, el objeto se desplaza o inclina en un ángulo con respecto a su posición original en la dirección horizontal.
• Sesgo Vertical o en eje "y": El sesgo vertical, por otro lado, se refiere a la deformación o inclinación del objeto en la dirección vertical, es decir, a lo largo del eje Y. Al aplicar un sesgo vertical, el objeto se desplaza o inclina en un ángulo con respecto a su posición original en la dirección vertical.

Ejemplos

• En este, se demuestra el sesgo en cada uno de los ejes, se puede notar una deformación en cada figura, respecto a la original que está en el origen del plano cartesiano.

• Se muestra un cuadrado sesgado verticalmente 30 grados sobre la esquina superior izquierda del cuadrado.